| |
A linear scale between the two smallest graduation marks is visualized and estimating the uncertain digit using this imaginary scale. Approximations to a linear scale are common: the distance between two points, the volume contained in a glass, how many yards the tailback gained on first down. Linear approximations are so common that the accuracy of the approximation is accurate to ±0.1 units. (For the case of the ruler used in the example: ±0.1 units * 0.1 cm = ±0.01 cm.)
In the example below, the orange solid is between 2.5 and 2.6 cm. However, the solid is clearly not 2.50 or 2.60 cm, and therefore a more accurate length could be recorded. An imaginary linear scale between the two graduation marks can be used to make a more accurate determination of the length. The edge of the solid is approximately 8/10 of the way between the 2.5 and 2.6 graduation marks. So, the uncertain digit is an "8", and the length to be recorded for the solid is 2.58±0.01 cm. The use of the "±" symbol indicates the uncertainty in the last digit.
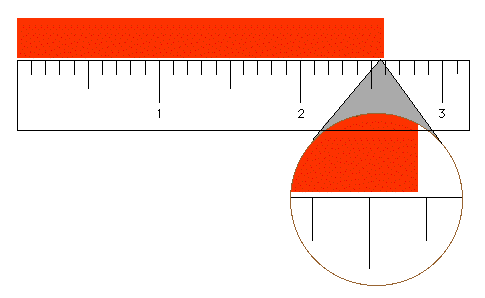
IMAGE. A ruler with a close-up view of the scale.
|
|