
|
|
|
|
|
|
|
|
|
|
|
|
|
|
 |
|
||||||||||||||
Diffraction |
|
Click the image in the left-hand column below to view the movie. Alternatively, you may use the buttons in the upper right to browse the movies. |
|
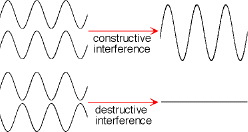 |
Waves Constructive interference occurs when waves are in phase; destructive interference occurs when the waves are out of phase with each other. (Companion Figure 4.2) |
 |
Optical transform slide The Discovery Optical Transform slide, obtainable from the Institute for Chemical Education. The 35-mm slide carries 8 photographically-reduced laser-written arrays. (Companion Demonstration 4.1) |
 |
Diffraction set up Diffraction can be viewed by shining a laser through an optical transform slide and observing the projected pattern. (Companion Demonstration 4.1) |
 |
Slide to eye Diffraction patterns can also be observed by directly viewing a light source through a slide (This is photographed by bringing the slide up to the camera lens.). (Companion Demonstration 4.2) |
 |
Diffraction lines Diffraction by an array of lines. The diffraction pattern shown is produced when the laser passes through the portion of the slide that is highlighted in red. What is the diffraction pattern of a horizontal array of lines? Of a vertical array of lines? Does an array with a smaller repeat distance give a diffraction pattern with a smaller repeat distance? (Companion Experiment 4) |
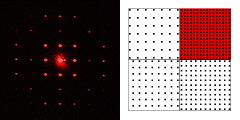 |
Diffraction square Diffraction by a square array. The diffraction pattern shown is produced when the laser passes through the portion of the slide that is highlighted in red. What is the diffraction pattern of a square array of dots? Does an array with a smaller repeat distance give a diffraction pattern with a smaller repeat distance? (Companion Experiment 4) |
 |
Diffraction square red and blue Diffraction patterns from a square array (see the previous movie) shown using two wavelengths of excitation, red 633-nm light from a He-Ne laser and blue 458-nm light from an argon ion laser; the longer wavelength results in wider spacings between diffraction spots. (Companion Demonstration 4.1) |
 |
Diffraction non-square Diffraction pattern from a square array (see the previous movie) shown using 458, 476, 488, 496, and 514-nm light from an argon ion laser excitation and red 633-nm light from a He-Ne laser; the longer wavelength results in wider spacings between diffraction spots. (Companion Demonstration 4.1) |
 |
Diffraction centered (red and blue) Diffraction by a non-square array. The diffraction pattern shown is produced when the laser passes through the portion of the slide that is highlighted in red. What is the diffraction pattern of a rectangular array of dots? Of a parallelogram array of dots where the angle is not 90 degrees? Of a hexagonal array of dots? How are the orientations of the diffraction patterns related to the orientations of the arrays of dots? (Companion Experiment 4) |
 |
Diffraction centered (increasing wavelength) Diffraction by a centered array. The diffraction pattern shown is produced when the laser passes through the portion of the slide that is highlighted in red. What happens if you put an additional dot in the array in the center of the unit cell? Does it matter if the dot placed in the center is or is not the same size as those in the original array? (Companion Experiment 4) |
 |
Diffraction triatomic Diffraction patterns from a centered array (see the previous movie) shown using two wavelengths of excitation, red 633-nm light from a He-Ne laser and blue 458-nm light from an argon ion laser; the longer wavelength results in wider spacings between diffraction spots. (Companion Demonstration 4.1) |
 |
Flashlight diffraction Diffraction pattern by identical size unit cells containing triatomic molecules with different bond angles. The positions of the diffraction spots depend only on the unit cell dimensions, and thus are identical for all these arrays. But the intensities of the diffraction spots depend on the atoms in the unit cell, and thus vary for these patterns. In some cases the differences are subtle. (Companion Figures 4.8 and 4.9) |
 |
Flashlight diffraction A flashlight bulb can be used to create a diffraction pattern by observing the bulb directly through a slide. (This is photographed by placing the optical transform slide directly in front of the camera lens.) (Companion Demonstration 4.2) |
 |
Powder diffraction Shining a laser through randomly-oriented slides containing identical square arrays creates a circular pattern of diffraction spots, which mimics what would be seen in the X-ray powder diffraction experiment. The diffraction pattern approaches that of the square arrays as the slides are rotated into alignment with one another. |
 |
PDMS diffraction stretch A laser is positioned to shine through a thin elastomer slab containing the square arrays of features on its surface. The PDMS slab is stretched by gently pulling the string. The diffraction pattern changes from square for the unstretched elastomer to rectangular upon stretching, demonstrating the reciprocal lattice effect. (JCE) |