Does ATP Provide Energy?

The conversion of adenosine triphosphate (ATP) into adenosine diphosphate (ADP) is an extremely important energy source for living organisms. Under common physiological conditions, it can be expressed as:

MgATP²⁻(aq) + H₂O(l) → MgADP⁻(aq) + HPO₄²⁻(aq) + H⁺(aq)

in which MgATP²⁻and MgADP⁻ represent the physiologically relevant magnesium complexes of ATP and ADP. I have found it interesting to use this reaction as an example when quantitatively discussing the Gibbs free energy.

Because the reaction in Equation 1 is used as an energy source, we would expect it to have a negative value of ΔG. We can calculate the standard Gibbs free energy, ΔG°_rxn, of the reaction using values of standard Gibbs free energies of formation, ΔG°_f, found in the literature (Table 1).

Table 1: Thermodynamic parameters for the species in Equation 1¹

Does APT Provide Energy Image 1

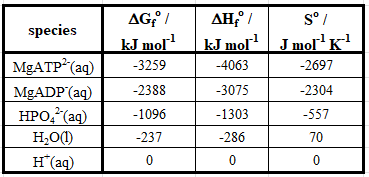
Table 1: Thermodynamic parameters for the species in Equation 1¹

To do so, we use the familiar equation:

$∆G_{rxn }^o= \sum ∆G_{f products}^o-\sum ∆G_{f reactants }^o$

Thus, for Equation 1 we find that ΔG°_rxn = +12 kJ mol^-1:

$∆G_{rxn }^o= \left[-2388 kJ {mol}^{-1}-1096 kJ {mol}^{-1}+0\right]-\left[-3529 kJ {mol}^{-1}-237 kJ {mol}^{-1}\right]$

Wait a minute…a positive Gibbs free energy indicates that this reaction is not spontaneous and can therefore provide no useful work to organisms. How is it that this reaction is used as an energy source for all of life on Earth?

The answer is that our calculation was done for standard conditions. However, we are interested in this reaction as it is carried out in living cells, which are not under standard conditions. Recall that standard conditions mean that all reactants and products are at 1 M concentration. So under standard conditions, [H⁺] = 1 M, which corresponds to pH = 0. Looking at Equation 1 and using the principle of Le Châtelier, it is seen that high concentrations of protons (on the product side) do not favor the reaction being spontaneous. However, this reaction normally occurs around pH = 7.2, corresponding to [H⁺] = 6 x 10^-8 M. That’s a proton concentration that’s over 10 million times lower than standard conditions! So let’s run this calculation using the conditions under which it usually takes place. To do so, we’ll use the equation:

$∆{\mathrm{G}}_{\mathrm{r}\mathrm{x}\mathrm{n}\mathrm{ }}=\mathbf{ }∆{\mathrm{G}}_{\mathrm{r}\mathrm{x}\mathrm{n}}^{\mathrm{o}}+\mathrm{R}\mathrm{T}\mathrm{l}\mathrm{n}\mathrm{Q}$

Where ΔG_rxn is the Gibbs free energy for reaction 1 under physiological conditions, T is the absolute temperature, R = 8.314 J mol^-1 K^-1, and Q is the reaction quotient for Equation 1:

$Q= \frac{\left[{MgADP}^{-}\right]\left[HP{O}_4^{2-}\right]\left[H^{+}\right]}{\left[{MgATP}^{2-}\right]}$

We’ll need the physiologically relevant concentrations^2,3 [MgATP^2-] = 3 mM, [MgADP^-] = 0.03 mM, HPO₄^2- = 5 mM, and H⁺ = 6 x 10^-8 M. We’ll also use T = 310 K (37°C).

Insertion of all these values into Equation 3 gives:

$∆{\mathrm{G}}_{\mathrm{r}\mathrm{x}\mathrm{n}\mathrm{ }}=\mathrm{ }12\mathrm{ }\mathrm{k}\mathrm{J}\mathrm{ }{\mathrm{m}\mathrm{o}\mathrm{l}}^{-1}+\left(8.314\mathrm{ }\mathrm{J}\mathrm{ }{\mathrm{m}\mathrm{o}\mathrm{l}}^{-1}{\mathrm{K}}^{-1}\right)\left(298\mathrm{ }\mathrm{K}\right)\mathrm{ }\mathrm{l}\mathrm{n}\frac{\left[0.00003\right]\left[.05\right]\left[6\mathrm{ }\mathrm{x}\mathrm{ }{10}^{-8}\right]}{\left[0.003\right]}$

Upon doing so, we find ΔG = -56 kJ mol^-1: spontaneous, and plenty of energy for the cell to do some work!

I have found that using this example in class provides a nice example of calculating the Gibbs free energy under both standard and non-standard conditions. It also provides a nice way to discuss the principle of Le Châtelier and to integrate biological sciences into the chemistry curriculum.

References:

• Alberty, R. A. Thermodynamics of the Hydrolysis of Adenosine Triphosphate as a Function of Temperature, pH, pMg, and Ionic Strength J. Phys. Chem. B 2003, 107, 12324-12330.
• Tantama, M.; Martínez-François, J. R.; Mongeon, R.; Yellen, G. Imaging Energy Status in Live Cells with a Fluorescent Biosensor of the Intracellular ATP-to-ADP Ratio. Nat. Commun. 2013, 4, 2550.
• Meyrat, A.; von Ballmoos, C. ATP Synthesis at Physiological Nucleotide Concentrations. Sci. Rep. 2019, 9, 3070.